GAN的相关知识主要是跟着李宏毅老师入门的,具体内容可以访问哔哩哔哩-李宏毅深度学习2017进行学习。这篇文章主要对学习内容进行总结。
1.传统生成模型
AutoEncoder
AutoEncoder是前馈神经网络的一种,曾经重要用于数据的降维或者特征的抽取,而现在也被广泛用于生成模型。与其他前馈神经网络不同的是,其他前馈神经网络关注的是Output Layer和错误率,而AutoEncoder关注点是Hidden Layer;并且普通前馈神经网络一般比较深,而AutoEncoder通常只有一层Hidden Layer。Hidden Layer中神经元组成的向量(Code)用来表示Input
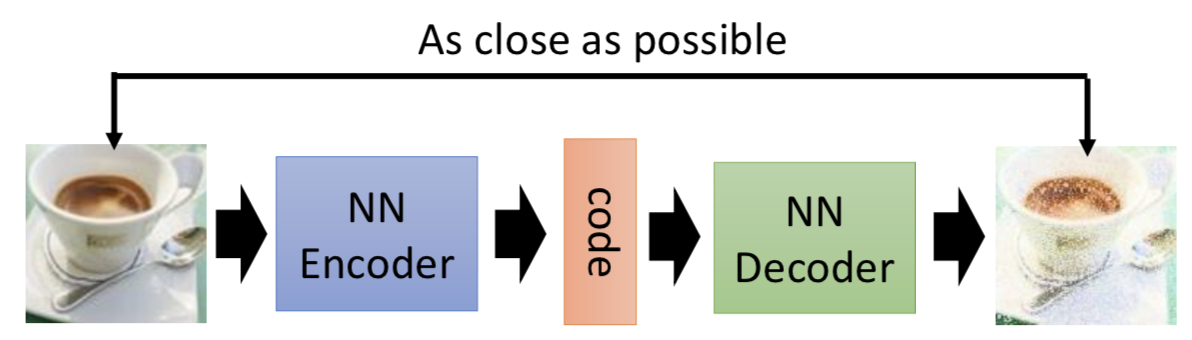
如图该模型的作用是生成与原图像相似的图像。将原始图像输入神经网络,经过Encoder的压缩,表示成Code;再经过Decoder的解压生成图像;最后计算生成图像与输入图像的MSE(Mean Square Error),这样就可以对模型进行训练。

若只取AutoEncoder的Decoder部分,随机生成Code向量输入网络进行解码,这样就可以生成图像。
但是从上图可以看出AutoEncoder的图像生成效果非常的差,从计算loss方式分析其原因。

可以从上图中看出,两幅图像仅仅一个像素点的位置不同,但是用MSE计算loss是一样大的,这就说明MSE不能衡量图像像素点的位置信息。
GAN就出场了,设计了Generator和Discriminator结构进行前馈运算,采用KL/JSD等方式,很好的解决了衡量两个图像分布之间‘difference’的问题。
2.GAN前馈流程图


初始化Generator和Discriminator网络参数,服从特定分布的随机变量输入Generator网络生成图像(标签为0),再和真实图像(标签为1)一块输入到Discriminator进行判断。
若是Discriminator对生成图像的判分较低,则Generator参数进行梯度下降更新(此时固定Discriminator);再将第二轮Generator生成的图像输入到Discriminator进行判断,若是Discriminator对其判分较高,则更新Discriminator参数。
3.GAN原理
给定真实数据分布$ P_{data}(x)$,此处的x代表真实图像构成的向量;设生成模型的分布$P_{G}(x;\theta)$,这个生成分布由$\theta$决定,生成图像模型的目标就是使得生成模型分布$P_{G}(x;\theta)$尽可能的接近真实数据分布$ P_{data}(x)$,也就是要计算$\theta$。
这样就可以采用最大似然估计的方法来,具体方法如下:
- 从真实数据分布$ P_{data}(x)$中采样得到${x^1,x^2,…,x^m}$;
- 计算每个数据的概率$P_G(x^i;\theta)$
- 计算似然:$L = \prod_{i=1}^mP_G(x^i;\theta)$
- 求得$\theta$使得似然最大化

使用最大似然估计求得$\theta$的过程如上图所示,对似然求log变成log似然;真实分布中的所有x的期望等价于概率积分,所以可以转化成积分运算,因为减号之后的积分与$\theta$无关,所以添加上去之后还是等价的;经过这样拼凑之后最大似然估计可以变成求两个分布之间的KL散度,两个分布越相似,KL散度值越小。
在求$\theta$之前必须要假定生成分布的类型,比如是高斯混合模型,但是在实践中这种假设的效果不太好,所以如何能设计出更加一般化的生成模型分布呢?
这里采用神经网络来产生生成分布$P_{G}(x;\theta)$,$\theta$也就是神经网络的权重参数。神经网络只要有非线性激活函数,理论上可以去拟合任意函数,概率分布也可以看作是函数映射,所以可以采用神经网络去学习复杂的概率分布。

Generator G
生成器G是一个函数,输入向量z,输出向量x
$P_{prior}(z)$表示输入向量z的先验分布,$P_G(x)$由生成器G决定
Discriminator D
判别器D是一个函数,输入向量x,输出标量值
D用来衡量$P_G(x)$与$P_{data}(x)$之间的不同
GAN公式
$G^*=arg\min\limits_{G}\max\limits_{D}V(G,D)$
$V=E_{x \sim P_{data}}[logD(x)]+E_{x \sim P_{G}}[log(1-D(x))]$ 衡量$P_G$与$P_{data}$的不同
在G一定的情况,寻找D使得$V(G,D)$最大化,也就是对于真实分布中的x,D(x)要接近1,对于生成分布中的x,D(x)要接近于0,这样使得判别器的能力增强;
再固定D,寻找G使得$\max\limits_{D}V(G,D)$最小,也就是让来自于生成分布中的x的D(x)尽可能的接近1,这样使得生成器的能力增强。
接下来对$G^*=arg\min\limits_{G}\max\limits_{D}V(G,D)$进行求解。
给定G,求得最优的$D^*$使得V最大。

接下来给定x,求$D^*$使得被积函数取极大值。$P_{data}(x)$和$P_{G}(x)$是已知值,只 需要对D求导即可得到极大值。

将$D^*$代入V式进行整理。

$log2P_{data}(x)$对x积分之后得$log2$,概率积分为1。

上图的推导主要是凑出JSD分布的形式,JS Divergence是KL散度的对称平滑版本,也是描述了两个分布之间的差异。因为JSD值域[0,log2]所以 $\max \limits_DV(G,D)$的取值范围为[-2log2,0]。
接下来的问题就是如何优化G,使得$P_G(x)$尽可能接近$P_{data}(x)$

如上图,将$\max \limits_DV(G,D)$视为损失函数$L(G)$,采用梯度下降的方法进行优化

4.GAN训练

如图所示,在实践训练中,我们不可能求得$P_G$和$P_{data}$的期望,所以只能从真实数据分布和生成数据分布中分别采样,代入到损失函数求的交叉熵。
具体的算法流程如下

5.问题优化

在生成模型的优化过程中,生成器的loss Function是$V=E_{x\sim P_{G}}[-log(1-D(x))]$。如上图所示,当D(x)接近0的时候,梯度非常的小。这就导致在训练的初期,生成器G如果想要骗过判别器D变化是非常的缓慢的。所以就将生成器的loss修改成$V=E_{x\sim P_{G}}[-log(D(x))]$这样可以提高训练的速度。
在实际训练中发现,loss一直不发生变化,即$\max \limits_DV(G,D)=0$
因为JSD值域是[0,log2],这也就是说明$P_G$和$P_{data}$没有相似之处,但是实际上两个分布是有相似之处的,出现问题的原因是我们在积分运算中国使用采样的方法,当训练过拟合的时候,D还是能把两部分的点给分开的,如下图所示。

我们是不是应该让D变得弱一点,减弱它的分类能力,但是我们的初衷是让D变得更强,这就产生了矛盾。
还有一种原因可能是,两个分布都是高维的,但是两个分布都十分的窄,交集相当的小,这就导致JSD比较大。
解决方法:添加噪声,让两个分布变得更宽一些,这样可以增大它们之间的交集,在训练过程中,再使噪声逐渐减小。

如上图所示,实际训练过程种可能出现这样的情况,真实的数据分布是双峰分布的,而生成的数据分布只拟合了其中一个峰的分布,也就是说没有学到整个分布。
造成这种情况的原因是,KL散度中两个分布写反了。

如上图所示,若是第一KL散度的写法,为了防止出现无穷大,所有有$P_{data}$出现的地方都必须有$P_G$覆盖,这样就不回出现Mode Collapse。